133 行代码实现质感地形
2016-09-18 算法爱好者
程序员们都喜欢创造一些东西,但是,还有什么会比创建一个世界更让人感到惊喜?想想Minecraft, Terragen, Skyrim,以及以前的每一个都会使用一些生成分形地形的飞行模拟器。今天,我们要来探索如何使用漂亮而又简单的QPSO算法 (diamond-square algorithm),到时,你也可以扮演上帝!
程序员往往是懒惰的(从经验来说的话),而懒惰的一个很好地“副作用”就是这真的是可以避免一些(重复)工作的很不错的方式。既然这样, 与其花上乏味的几个小时来创建可能是很蹩脚的岩石表面,不如我们在思想上教会电脑岩石到底是什么。为了达到我们的目的,我们会生成分形或者形状,而这些形状会以越来越小的变化不断重复。
我并不能以某种方式来证明地形确实是分形的,但是这种方法看起来真的很不错,因此你可以信任这种方法。

立体地图
我们会将我们的地形存储为一个简单地立体地图:一个由地形在任意给定的x,y坐标上的高度值所组成的二维数组。这是一个比较简单的数据结构,用我们喜欢的canvas,webgl,interpretive dance等技术都可以来渲染这些高度值。最大的限制是我们不能在地形中表示有垂直的洞的形状,比如洞穴,隧道或者桥梁。

对应的算法
对任何尺寸的网格你都可以应用上面的算法来生成地图,但是对于一个由2的整数幂加1的网格组成方形来说它是最简单的。我们将使用x、y和z轴相同大小的值,在一个多维数据集中实现我们的地形。我们把相关的细节(detail)(即网格的数量)转化成了2的整数幂加1,因此更多的网格数量需要有更大的数据集。
想法是这样的:取一个平面的方形。把它分成4个子方形,然后把这4个子方形的中心向上或向下随机的偏移一定量。把这些子方形再分成更多的子方形并且重复上面的步骤,每一次都将偏移的量减少,这样第一次的偏移会有最大的效果而后面的偏移都会提供更小的细节(起伏程度)。
这就是中点置换算法。我们的菱形算法基于类似的原则,但是生成了看起来会更自然的结果。与其只是把方格分成更多的子方格,不如在分成子方格与分成子的菱形方格之间做个替换。
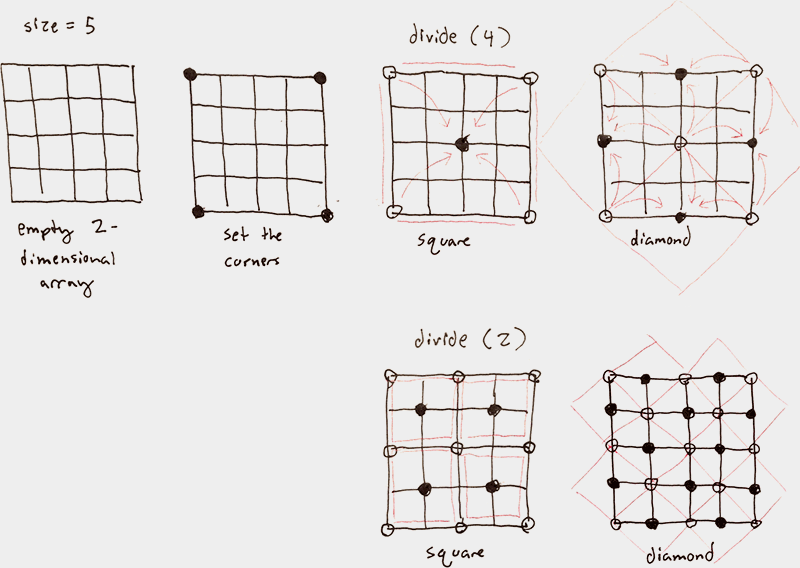
1.设置各个角的坐标
首先,我们要设置各个角的坐标值来作为“种子”值,它会影响后面的呈现。我们会将所有的角落从数据集的一半的位置开始:
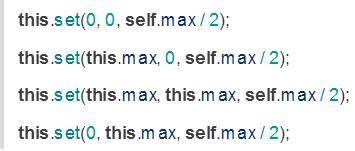
2.将地图分块
现在,我们将会递归的来看立体地图的越来越小的分块。在每一个分块的过程中,我们会把地图分成方块,并在方形阶段更新它们的中心点。然后,我们会把地图分成菱形,并在菱形阶段再次更新它们的中心点。

saele变量保证了随着我们分块的次数的增多,偏移量是不断减小的。对于每一次分块,我们将当前的size变量与roughness相乘,roughness决定了我们的地形是平滑的(该变量值趋近于0时)还是起伏的(该变量值趋近于1时)。
3.形状
两种形状(方形和菱形)的工作机制是类似的,但是要从不同的点来绘制数据。在方形阶段,要在应用随机偏移之前获取四个角的坐标的平均值,在菱形阶段要在执行随机偏移之前获取四个边缘点的坐标的平均值。

渲染
算法只是给了我们数据,我们可以用很多种方式来渲染数据。我们将整合一连串的渲染技巧来渲染一个位于canvas元素上的栅格化的,等距的,3d形式的地形图上。
从back到front
首先,我们将创建嵌套的循环从我们地图的“back”(y = 0) 到“front”(y=this.size)来绘制矩形。如果你要渲染一个简单地,平的,自顶向下的方形,那么要执行的循环是一样的。

光亮和阴影
我们对于集合映射的原始方法提供了一个很好的视觉文理。通过比较当前的高度值和下一个点的高度值,我们会找到一个坡度。坡度高的一侧我们用较亮的矩形来填充,另一侧则用较暗的矩形来填充。

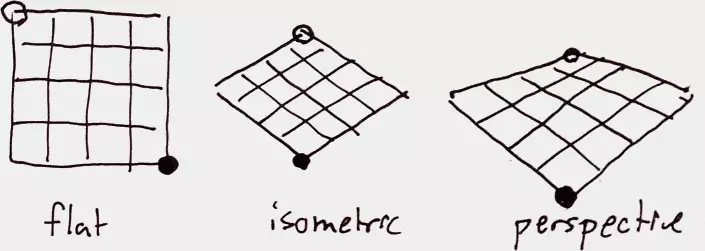
等轴投影
我们可以从正面来绘制每一样东西,但是,在将方块转为3d之前,先将它转为菱形看起来会更有趣。等轴投影将左上角和右下角在视图的中间对齐。

透视投影
我们将使用一个同样简单的3d投影转换我们的x,y,z值为在二维视角屏幕上的平面图像。
所有的透视投影的基本想法都是用水平和垂直的位置除以深度,那样的话更高的深度的渲染就会更接近于原点(例如,越远的物体就会看起来越小)。

把所有的内容整合起来
首先,我们用我们所期望的细小平面创建了一个地形实例。然后我们生成了它的立体地图,提供了一个位于0和1之间的roughness值。最后,我们把地形绘制到了canvas上。












